How Does The Size Of Oxygens Nucleus Affect The Distribution

Nuclear Physics

73 Backdrop of Nuclei

Learning Objectives

Past the end of this section, you lot will be able to:

Describe the composition and size of an atomic nucleus
Use a nuclear symbol to limited the composition of an atomic nucleus
Explain why the number of neutrons is greater than protons in heavy nuclei
Calculate the atomic mass of an element given its isotopes

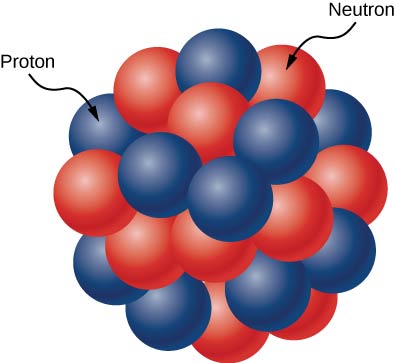
The atomic nucleus is composed of protons and neutrons ((Effigy)). Protons and neutrons accept approximately the aforementioned mass, but protons acquit one unit of positive accuse $\left(\text{+}e\right),$ and neutrons comport no charge. These particles are packed together into an extremely pocket-size space at the center of an atom. According to scattering experiments, the nucleus is spherical or oblong in shape, and about i/100,000th the size of a hydrogen cantlet. If an atom were the size of a major league baseball stadium, the nucleus would be roughly the size of the baseball. Protons and neutrons within the nucleus are called nucleons.

The atomic nucleus is composed of protons and neutrons. Protons are shown in bluish, and neutrons are shown in red.

The figure shows a cluster of red and blue spheres packed closely together. The red spheres are labeled neutrons and the blue ones protons.

Counts of Nucleons

The number of protons in the nucleus is given by the atomic number, Z. The number of neutrons in the nucleus is the neutron number, N. The full number of nucleons is the mass number, A. These numbers are related by

$A=Z+N.$

A nucleus is represented symbolically past

${}_{Z}^{A}\text{X},$

where X represents the chemical element, A is the mass number, and Z is the atomic number. For instance, ${}_{\phantom{\rule{0.5em}{0ex}}6}^{12}\text{C}$ represents the carbon nucleus with half dozen protons and 6 neutrons (or 12 nucleons).

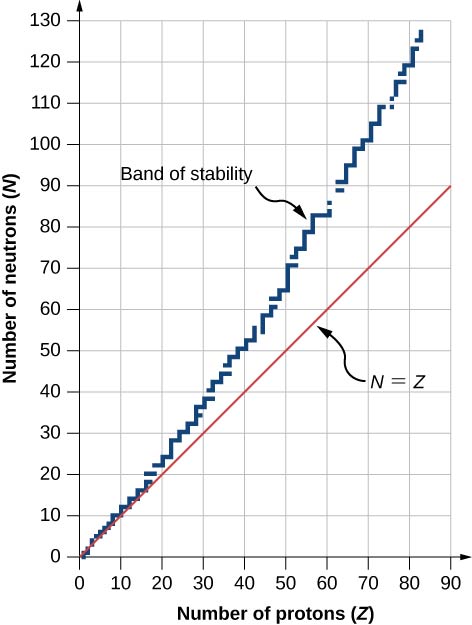
A graph of the number N of neutrons versus the number Z of protons for a range of stable nuclei (nuclide s) is shown in (Effigy). For a given value of Z, multiple values of North (blueish points) are possible. For pocket-sized values of Z, the number of neutrons equals the number of protons $\left(N=P\right),$ and the information fall on the red line. For large values of Z, the number of neutrons is greater than the number of protons $\left(N>P\right),$ and the data points fall above the red line. The number of neutrons is mostly greater than the number of protons for $Z>15.$

This graph plots the number of neutrons Due north against the number of protons Z for stable atomic nuclei. Larger nuclei, have more neutrons than protons.

A graph showing number of neutrons, N versus number of protons, Z. A straight line on the graph is labeled N equal to Z. Another, jagged line, is labeled band of stability. This has incremental steps. It starts at the origin. At Z = 80, the value of N is 120.

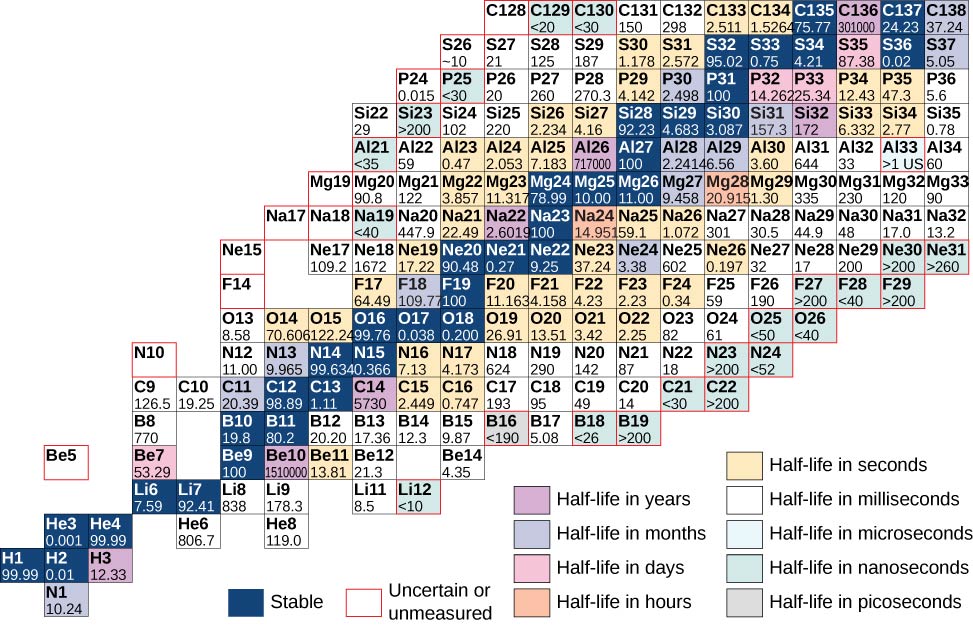
A nautical chart based on this graph that provides more detailed information about each nucleus is given in (Effigy). This chart is called a chart of the nuclides. Each cell or tile represents a divide nucleus. The nuclei are arranged in order of ascending Z (along the horizontal direction) and ascending N (along the vertical direction).

Fractional chart of the nuclides. For stable nuclei (night bluish backgrounds), cell values represent the per centum of nuclei establish on Earth with the aforementioned atomic number (pct affluence). For the unstable nuclei, the number represents the half-life.

Figure shows a chart of nuclides, with ascending Z along the horizontal direction and ascending N along the vertical direction. The cells along diagonal in the centre of the chart are color coded to indicate that they are stable.

Atoms that comprise nuclei with the same number of protons (Z) and dissimilar numbers of neutrons (North) are chosen isotopes. For example, hydrogen has 3 isotopes: normal hydrogen (1 proton, no neutrons), deuterium (one proton and one neutron), and tritium (one proton and two neutrons). Isotopes of a given atom share the aforementioned chemical properties, since these properties are determined by interactions betwixt the outer electrons of the cantlet, and not the nucleons. For example, water that contains deuterium rather than hydrogen ("heavy water") looks and tastes like normal water. The following table shows a list of common isotopes.

Common Isotopes*No entry if less than 0.001 (trace amount).
**Stable if half-life > 10 seconds.
Element	Symbol	Mass Number	Mass (Atomic Mass Units)	Percent Abundance*	One-half-life**
Hydrogen	H	1	1.0078	99.99	stable
	${}^{2}\text{H}\phantom{\rule{0.2em}{0ex}}\text{or}\phantom{\rule{0.2em}{0ex}}\text{D}$	2	2.0141	0.01	stable
	${}^{3}\text{H}$	iii	3.0160	−	12.32 y
Carbon	${}^{12}\text{C}$	12	12.0000	98.91	stable
	${}^{13}\text{C}$	13	13.0034	1.1	stable
	${}^{14}\text{C}$	14	14.0032	−	5730 y
Nitrogen	${}^{14}\text{N}$	14	fourteen.0031	99.half-dozen	stable
	${}^{15}\text{N}$	15	xv.0001	0.4	stable
	${}^{16}\text{N}$	sixteen	16.0061	−	7.13 south
Oxygen	${}^{16}\text{O}$	16	15.9949	99.76	stable
	${}^{17}\text{O}$	17	16.9991	0.04	stable
	${}^{18}\text{O}$	eighteen	17.9992	0.20	stable
	${}^{19}\text{O}$	19	19.0035	−	26.46 s

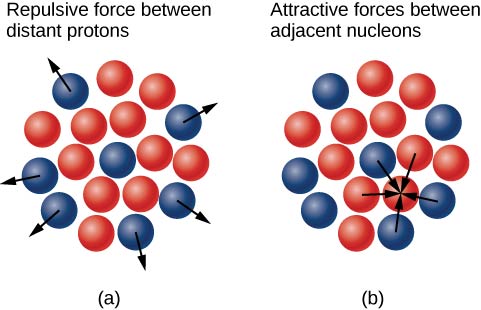
Why do neutrons outnumber protons in heavier nuclei ((Effigy))? The answer to this question requires an agreement of forces inside the nucleus. Ii types of forces be: (1) the long-range electrostatic (Coulomb) strength that makes the positively charged protons repel one another; and (ii) the short-range stiff nuclear strength that makes all nucleons in the nucleus concenter 1 another. Y'all may besides have heard of a "weak" nuclear forcefulness. This force is responsible for some nuclear decays, but every bit the name implies, it does not play a office in stabilizing the nucleus against the strong Coulomb repulsion information technology experiences. Nosotros discuss strong nuclear force in more detail in the next chapter when nosotros cover particle physics. Nuclear stability occurs when the attractive forces between nucleons recoup for the repulsive, long-range electrostatic forces between all protons in the nucleus. For heavy nuclei $\left(Z>15\right),$ excess neutrons are necessary to keep the electrostatic interactions from breaking the nucleus apart, as shown in (Figure).

(a) The electrostatic force is repulsive and has long range. The arrows represent outward forces on protons (in blue) at the nuclear surface past a proton (also in blue) at the centre. (b) The strong nuclear force acts betwixt neighboring nucleons. The arrows represent attractive forces exerted by a neutron (in red) on its nearest neighbors.

Figure a shows a cluster of small red and blue circles. There is a blue proton in the center, surrounded by red neutrons. There are more protons at the periphery, which have arrows pointing outwards. Figure b shows the same cluster. Arrows show both protons and neutrons being attracted towards an adjacent neutron.

Because of the beingness of stable isotopes, we must take special intendance when quoting the mass of an element. For example, Copper (Cu) has two stable isotopes:

${}_{29}^{63}\text{C}\text{u}\phantom{\rule{0.2em}{0ex}}\left(62.929595\phantom{\rule{0.2em}{0ex}}\text{g/mol}\right)\phantom{\rule{0.2em}{0ex}}\text{with an abundance of}\phantom{\rule{0.2em}{0ex}}69.09\text{%}$

${}_{29}^{65}\text{C}\text{u}\phantom{\rule{0.2em}{0ex}}\left(64.927786\phantom{\rule{0.2em}{0ex}}\text{g/mol}\right)\phantom{\rule{0.2em}{0ex}}\text{with an abundance of}\phantom{\rule{0.2em}{0ex}}30.91\text{%}$

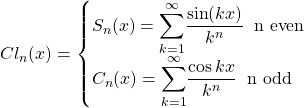
Given these 2 "versions" of Cu, what is the mass of this element? The atomic mass of an chemical element is defined equally the weighted average of the masses of its isotopes. Thus, the diminutive mass of Cu is ${m}_{\text{Cu}}=\left(62.929595\right)\left(0.6909\right)\phantom{\rule{0.2em}{0ex}}+\phantom{\rule{0.2em}{0ex}}\left(64.927786\right)\left(0.3091\right)=63.55\phantom{\rule{0.2em}{0ex}}\text{g/mol}.$ The mass of an private nucleus is often expressed in diminutive mass unit due south (u), where $\text{u}=1.66054\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-27}\text{kg}$ . (An atomic mass unit of measurement is divers as 1/12th the mass of a ${}^{12}\text{C}$ nucleus.) In atomic mass units, the mass of a helium nucleus (A = 4) is approximately four u. A helium nucleus is as well chosen an alpha (α) particle.

Nuclear Size

The simplest model of the nucleus is a densely packed sphere of nucleons. The volume V of the nucleus is therefore proportional to the number of nucleons A, expressed past

$V=\frac{4}{3}\phantom{\rule{0.2em}{0ex}}\pi {r}^{3}=kA,$

where r is the radius of a nucleus and chiliad is a constant with units of volume. Solving for r, nosotros accept

$r={r}_{0}{A}^{1\text{/}3}$

where ${r}_{0}$ is a constant. For hydrogen ( $A=1$ ), ${r}_{0}$ corresponds to the radius of a single proton. Scattering experiments support this general relationship for a broad range of nuclei, and they imply that neutrons accept approximately the same radius as protons. The experimentally measured value for ${r}_{0}$ is approximately 1.2 femtometer (recall that $1\phantom{\rule{0.2em}{0ex}}\text{fm}={10}^{-15}\text{m}$ ).

The Iron NucleusFind the radius (r) and approximate density ( $\rho$ ) of a Fe-56 nucleus. Assume the mass of the Fe-56 nucleus is approximately 56 u.

Strategy (a) Finding the radius of ${}^{56}\text{Fe}$ is a straightforward awarding of $r={r}_{0}{A}^{1\text{/}3}$ , given $A=56.$ (b) To find the approximate density of this nucleus, assume the nucleus is spherical. Calculate its book using the radius constitute in part (a), and then notice its density from $\rho =m\text{/}V.$

Solution

The radius of a nucleus is given by

$r={r}_{0}{A}^{1\text{/}3}.$

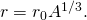
Substituting the values for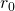 ${r}_{0}$ and A yields

$\begin{array}{cc}\hfill r& =\left(1.2\phantom{\rule{0.2em}{0ex}}\text{fm}\right){\left(56\right)}^{1\text{/}3}=\left(1.2\phantom{\rule{0.2em}{0ex}}\text{fm}\right)\left(3.83\right)\hfill \\ & =4.6\phantom{\rule{0.2em}{0ex}}\text{fm}.\hfill \end{array}$
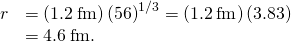
Density is defined to be $\rho =m\text{/}V,$ which for a sphere of radius r is

$\rho =\frac{m}{V}=\frac{m}{\left(4\text{/}3\right)\text{π}{r}^{3}}.$

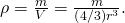
Substituting known values gives

$\rho =\frac{56\phantom{\rule{0.2em}{0ex}}\text{u}}{\left(1.33\right)\left(3.14\right){\left(4.6\phantom{\rule{0.2em}{0ex}}\text{fm}\right)}^{3}}=0.138\phantom{\rule{0.2em}{0ex}}{\text{u/fm}}^{3}.$

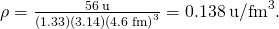
Converting to units of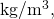 $\text{kg}\text{/}{\text{m}}^{3},$ we find

$\rho =\left(0.138\phantom{\rule{0.2em}{0ex}}{\text{u/fm}}^{3}\right)\left(1.66\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-27}\phantom{\rule{0.2em}{0ex}}\text{kg/u}\right)\left(\frac{1\phantom{\rule{0.2em}{0ex}}\text{fm}}{{10}^{-15}\phantom{\rule{0.2em}{0ex}}\text{m}}\right)=2.3\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{17}\phantom{\rule{0.2em}{0ex}}{\text{kg/m}}^{3}.$

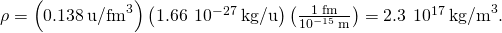
Significance

The radius of the Fe-56 nucleus is found to be approximately 5 fm, and so its diameter is nigh x fm, or 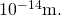${10}^{-14}\text{m}.$ In previous discussions of Rutherford's handful experiments, a calorie-free nucleus was estimated to be 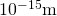${10}^{-15}\text{m}$ in bore. Therefore, the result shown for a mid-sized nucleus is reasonable.
The density found here may seem incredible. However, it is consequent with earlier comments about the nucleus containing virtually all of the mass of the cantlet in a tiny region of space. One cubic meter of nuclear matter has the aforementioned mass equally a cube of water 61 km on each side.

Cheque Your Agreement Nucleus X is two times larger than nucleus Y. What is the ratio of their atomic masses?

eight

Summary

The diminutive nucleus is composed of protons and neutrons.
The number of protons in the nucleus is given by the atomic number, Z. The number of neutrons in the nucleus is the neutron number, North. The number of nucleons is mass number, A.
Atomic nuclei with the same atomic number, Z, merely dissimilar neutron numbers, Due north, are isotopes of the same chemical element.
The atomic mass of an chemical element is the weighted average of the masses of its isotopes.

Conceptual Questions

Ascertain and make clear distinctions between the terms neutron, nucleon, nucleus, and nuclide.

The nucleus of an cantlet is made of 1 or more nucleons. A nucleon refers to either a proton or neutron. A nuclide is a stable nucleus.

What are isotopes? Why do isotopes of the same atom share the aforementioned chemic properties?

Problems

The mass (K) and the radius (r) of a nucleus can be expressed in terms of the mass number, A. (a) Show that the density of a nucleus is independent of A. (b) Calculate the density of a gilded (Au) nucleus. Compare your answer to that for atomic number 26 (Fe).

a. $r={r}_{0}{A}^{1\text{/}3},\rho =\frac{3\phantom{\rule{0.2em}{0ex}}\text{u}}{4\pi {r}_{0}{}^{3}}$ ;
b. $\begin{array}{ccc}\hfill \rho & =\hfill & 2.3\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{17}\phantom{\rule{0.2em}{0ex}}{\text{kg/m}}^{3}\hfill \end{array}$

A particle has a mass equal to 10 u. If this mass is converted completely into energy, how much free energy is released? Express your reply in mega-electron volts (MeV). (Recall that $1\phantom{\rule{0.2em}{0ex}}\text{eV}=1.6\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-19}\text{J}$ .)

Find the length of a side of a cube having a mass of i.0 kg and the density of nuclear matter.

side length $=1.6\phantom{\rule{0.2em}{0ex}}\text{μm}$

The detail that you can detect using a probe is limited by its wavelength. Calculate the energy of a particle that has a wavelength of $1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-16}\text{m}$ , small-scale plenty to notice details nearly one-tenth the size of a nucleon.